
Галерея поверхностей
Галерея математических поверхностей находится здесь. Выбрав поверхность для просмотра вы можете также покрутить ее мышкой на экране.

Открыты трехмерные солитоны
После тридцатилетнего поиска найдены нелинейные дифференциальные уравнения, обладающие трехмерными солитонными решениями. Ключевой стала идея «комплексификации» времени, которая может найти дальнейшие приложения в теоретической физике.
При изучении какой-либо физической системы вначале идет этап «первоначального накопления» экспериментальных данных и их осмысление. Затем эстафета передается теоретической физике. Задача физика-теоретика состоит в том, чтобы на основании накопленных данных вывести и решить математические уравнения для этой системы. И если первый шаг, как правило, не представляет особой проблемы, то второй — точное решение полученных уравнений — зачастую оказывается несравненно более трудной задачей.
Продолжение – в источнике на “Элементах”.
Геометрия мыльных пузырей до сих пор озадачивает математиков

Как соединить два мыльных пузыря, чтобы минимизировать их суммарную площадь поверхности (включая перегородку)? Ответ на этот вопрос интуитивно очевиден, но строгое математическое решение этой задачи было дано лишь в 2000 году. Тот же вопрос для трех и более пузырей до сих пор остается открытым. Немногим лучше обстоит дело и в плоском случае. Несмотря на все достижения математики, геометрия пузырьковых кластеров остается очень сложной задачей.
Продолжение статьи с Элементов здесь.
Весна на фрактальной улице

Из фрактального сообщества “Вконтакте.ру”
Фрактальная капуста

Выросла в блоге dxdt.ru
Однополосный гиперболоид
Один из красивейших фонтанов Ташкента на пересечении улиц Носыра (бывшая Ш. Руставели) и Бабура (бывшая Б. Хмельницкого). Когда-то на этом месте стоял памятник Ленину, фонтан гораздо лучше  . Наклонные струи, расположенные на окружности, огибают поверхность, называемую “однополостный гиперболоид”. В зависимости от угла наклона линий она может изменяться от цилиндра до конуса или до плоскости, попробуйте пофантазировать на эту тему.
. Наклонные струи, расположенные на окружности, огибают поверхность, называемую “однополостный гиперболоид”. В зависимости от угла наклона линий она может изменяться от цилиндра до конуса или до плоскости, попробуйте пофантазировать на эту тему.
Вопрос для тех, кто не потерял способность мыслить от жары. При каком угле с вертикалью струи воды талия гиперболоида имеет минимальный радиус? (Наклон струи в плоскости, касательной к окружности основания в точке выхода струи).
Фото Баламута
Красота! И все таки человек может не только разрушать! Как Вы считаете?
Кельтский орнамент

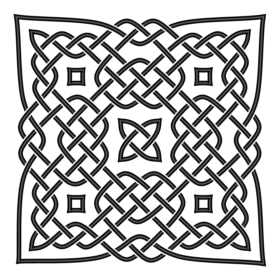
Рассмотрите внимательно первый рисунок – можно ли его нарисовать не отрывая руки от бумаги? И второй – кроме пяти маленьких вставок – это одна линия или несколько? Сможете ли повторить? А по памяти? 
Ну как? Получилось?
Удивительные галереи
На этом сайте, стоит посмотреть его картины, например, такие:


Вам нравиться? Поделитесь комментарием. Он вверху!
Мозаика Регистана

Это мозаика одной из мечетей на площади Регистан в Самарканде. Рассмотрите десятиугольник в центре – как он построен? Для подсказки статья Опубликовано в "Информационном Буме" о правильных многоугольниках.










