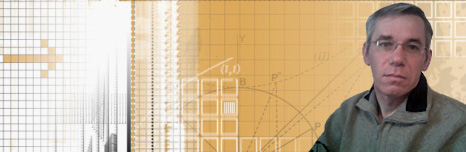

Однополосный гиперболоид
Один из красивейших фонтанов Ташкента на пересечении улиц Носыра (бывшая Ш. Руставели) и Бабура (бывшая Б. Хмельницкого). Когда-то на этом месте стоял памятник Ленину, фонтан гораздо лучше  . Наклонные струи, расположенные на окружности, огибают поверхность, называемую “однополостный гиперболоид”. В зависимости от угла наклона линий она может изменяться от цилиндра до конуса или до плоскости, попробуйте пофантазировать на эту тему.
. Наклонные струи, расположенные на окружности, огибают поверхность, называемую “однополостный гиперболоид”. В зависимости от угла наклона линий она может изменяться от цилиндра до конуса или до плоскости, попробуйте пофантазировать на эту тему.
Вопрос для тех, кто не потерял способность мыслить от жары. При каком угле с вертикалью струи воды талия гиперболоида имеет минимальный радиус? (Наклон струи в плоскости, касательной к окружности основания в точке выхода струи).
Фото Баламута
Красота! И все таки человек может не только разрушать! Как Вы считаете?
С экрана на стол

Миссия Shapeways благородна — реализовать мечту простого 3D-дизайнера о том, чтобы подержать в руках смоделированное на компьютере. Более того, новая компания планирует делать это массово, доступно и постоянно.
Схема действия сервиса проста: сделали дизайн — выбрали материал — заплатили и подождали несколько дней — получили посылку с объектами, сделанными в точности по собственной модели. Печать на 3D-принтерах, которая является здесь способом материализации, известна своей дороговизной. В связи с этим главное достижение Shapeways — довольно низкая для технологии стоимость изготовления, поддерживать которую планируется за счёт большого числа заказов и, соответственно, немалых объёмов производства.
При этом создатели проекта обещают не просто быть выгодной 3D-типографией, но сделать всё возможное для формирования активного сообщества людей, интересующихся трёхмерным моделированием и пробующих в нём свои силы. Пока проект находится в стадии бета-тестирования, и аккаунты раздаются по приглашениям, но узнать подробности и посмотреть на примеры сделанного можно без регистрации.
Ссылка по теме (eng): Shapeways.com Найдено на Эксперимент.ру
Кельтский орнамент

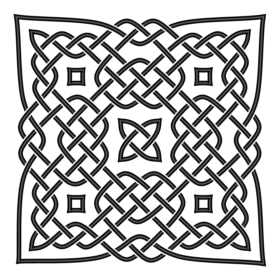
Рассмотрите внимательно первый рисунок – можно ли его нарисовать не отрывая руки от бумаги? И второй – кроме пяти маленьких вставок – это одна линия или несколько? Сможете ли повторить? А по памяти? 
Ну как? Получилось?
Удивительные галереи
На этом сайте, стоит посмотреть его картины, например, такие:


Вам нравиться? Поделитесь комментарием. Он вверху!
Вулкан и замощение плоскости
Сера в комбинации с другими минералами окрашивает кратер вулкана Даллол, находящегося в Эфиопии, в зеленоватые оттенки. Даллол находится на отметке 48 метров ниже уровня моря и является самым низким расположенным на суше вулканом.

Обратите внимание на то, как природа замостила плоскость – сколькиугольники для этого использованы? 
Мозаика Регистана

Это мозаика одной из мечетей на площади Регистан в Самарканде. Рассмотрите десятиугольник в центре – как он построен? Для подсказки статья Опубликовано в "Информационном Буме" о правильных многоугольниках.
Объемы кожуры и мякоти равны

Подробнее – на Этюдах
Спиральный дом

А здесь большая галерея разных спиралей в природе и в технике. Рекомендую взглянуть.







